VPC Lattice: yet another connectivity option or a game-changer?
12 April 2024 - 4 min. read
Damiano Giorgi
DevOps Engineer
 Applications running in production lose their ability to tell us directly what is going on under the hood, they become like black boxes and so we need a way to trace and monitor their behavior. Logging is by far the simplest and most straightforward approach to do so. We instruct the program during development to emit information while running that will be useful for future troubleshooting or simply for analysis.When it comes to Python, the built-in module for logging is designed to fit into applications with minimal setup. Whether you’ve already mastered logging in Python or you are starting to develop with it, the aim of this article is to be as comprehensive as possible and to dive into methodologies to leverage logging potentials. Note that this is a two-part article. In the second part, we will approach AWS services and use a combination of AWS Kinesis Data Firehose and AWS ElasticSearch Service to provide a way to show and debug logs on Kibana Dashboard as well as storing them to S3 to have long term copies at hand.
Applications running in production lose their ability to tell us directly what is going on under the hood, they become like black boxes and so we need a way to trace and monitor their behavior. Logging is by far the simplest and most straightforward approach to do so. We instruct the program during development to emit information while running that will be useful for future troubleshooting or simply for analysis.When it comes to Python, the built-in module for logging is designed to fit into applications with minimal setup. Whether you’ve already mastered logging in Python or you are starting to develop with it, the aim of this article is to be as comprehensive as possible and to dive into methodologies to leverage logging potentials. Note that this is a two-part article. In the second part, we will approach AWS services and use a combination of AWS Kinesis Data Firehose and AWS ElasticSearch Service to provide a way to show and debug logs on Kibana Dashboard as well as storing them to S3 to have long term copies at hand.logger.info("Logging a variable %s", variable1)we are describing the following situation: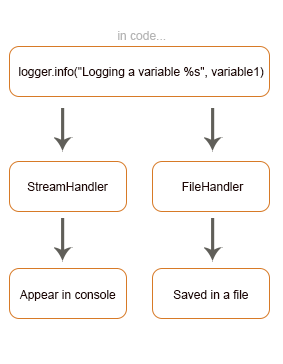 Python’s standard library comes with a logging module that you can start using without installing anything.In order to adhere to best practices which request avoiding to simply print into console whatever you want to report, Python’s logging module offers multiple advantages:
Python’s standard library comes with a logging module that you can start using without installing anything.In order to adhere to best practices which request avoiding to simply print into console whatever you want to report, Python’s logging module offers multiple advantages:basicConfig().
import logging
logging.basicConfig(level=logging.DEBUG,
filename='basic_config_test1.log',
format='%(asctime)s %(levelname)s:%(message)s')
def basic_config_test1():
logging.debug("debug log test")
logging.error("error log test")
Running the previous code, a new basic_config_test1.log file will be generated with the following content, except for the date, which depends obviously on the execution time.2020-05-08 17:19:29,220 DEBUG:debug log test 2020-05-08 17:19:29,221 ERROR:error log testNOTE: basicConfig only works the first time it is called in a runtime. If you have already configured your root logger, calling basicConfig will have no effect.DEBUG-level logs are now visible, and logs are printed with the following custom structure:
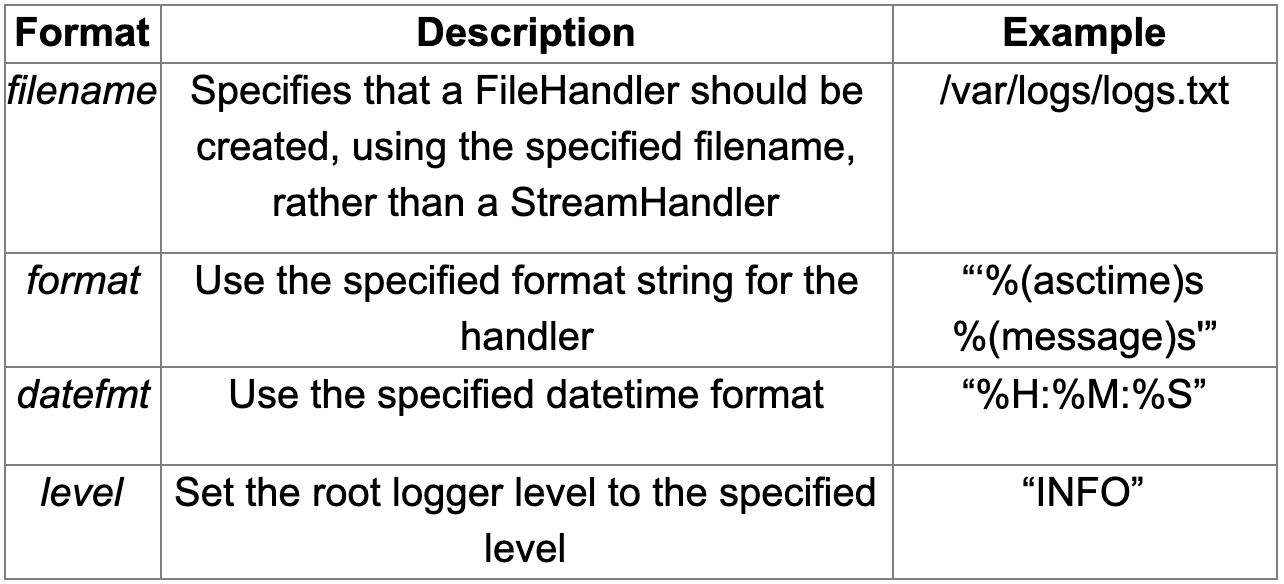 This is a simple and practical way to configure small scripts. Following Python best practices we recommend managing a logger instance for each module of your application, but it is understandable that this can be challenging and unclean by using basicConfig() capabilities alone. So we will next focus on how to improve a basic logging solution.
This is a simple and practical way to configure small scripts. Following Python best practices we recommend managing a logger instance for each module of your application, but it is understandable that this can be challenging and unclean by using basicConfig() capabilities alone. So we will next focus on how to improve a basic logging solution.logger = logging.getLogger(__name__)This method creates a new custom logger, different from the root one. The ß argument corresponds to the fully qualified name of the module from which this method is called. This allows you to also take into consideration the logger’s name as part of each log row by dynamically setting that name to match the one of the current modules you’re working with.It is possible to recover a logger's name property with %(name)s as shown in the following example.
# logging_test1.py
import logging
logging.basicConfig(level=logging.DEBUG,
filename='basic_config_test1.log',
format='%(asctime)s %(name)s %(levelname)s:%(message)s')
logger = logging.getLogger(__name__)
def basic_config_test1():
logger.debug("debug log test 1")
logger.error("error log test 1")
# logging_test2.py
import logging
import logging_test1
logger = logging.getLogger(__name__)
def basic_config_test2():
logger.debug("debug log test 2")
logger.error("error log test 2")
We have a better configuration now, each module is describing itself inside the log stream and everything is more clear, but nonetheless, the logger instantiated in the logging_test2 module will use the same configuration as the logger instantiated in the logging_test1 module, i.e. the root logger’s configuration. As stated before, the second invocation of basicConfig() method will have no effect. Therefore, executing both basic_config_test1() and basic_config_test2()methods will result in the creation of a single basic_config_test1.log file with the following content.2020-05-09 19:37:59,607 logging_test1 DEBUG:debug log test 1 2020-05-09 19:37:59,607 logging_test1 ERROR:error log test 1 2020-05-09 19:38:05,183 logging_test2 DEBUG:debug log test 2 2020-05-09 19:38:05,183 logging_test2 ERROR:error log test 2Depending on the context of your application, using a single configuration for loggers instantiated in different modules can be not enough.In the next section, we will see how to provide logging configuration across multiple loggers through either fileConfig() or dictConfig().
[loggers] keys=root,secondaryThe keys are used to traverse the file and read appropriate configurations for each section. The keys are defined as [_], where the section name is logger, handler, or formatter which are predefined as said before.A sample logging configuration file (logging.ini) is shown below.
[loggers] keys=root,custom [handlers] keys=fileHandler,streamHandler [formatters] keys=formatter [logger_root] level=DEBUG handlers=fileHandler [logger_custom] level=ERROR handlers=streamHandler [handler_fileHandler] class=FileHandler level=DEBUG formatter=formatter args=("/path/to/log/test.log",) [handler_streamHandler] class=StreamHandler level=ERROR formatter=formatter [formatter_formatter] format=%(asctime)s %(name)s - %(levelname)s:%(message)sPython’s best practices recommend to only maintain one handler per logger relying on the inheritance of child logger for properties propagation. This basically means that you just have to attach a specific configuration to a parent logger, to have it inherited by all the child loggers without having to set it up for every single one of them. A good example of this is a smart use of the root logger as the parent.Back on track, once you have prepared a configuration file, you can attach it to a logger with these simple lines of code:
import logging.config
logging.config.fileConfig('/path/to/logging.ini',
disable_existing_loggers=False)
logger = logging.getLogger(__name__)
In this example, we also included disable_existing_loggers set to False, which ensure that pre-existing loggers are not removed when this snippet is executed; this is usually a good tip, as many modules declare a global logger that will be instantiated before fileConfig() is called.import logging.config
config = {
"version": 1,
"disable_existing_loggers": False,
"formatters": {
"standard": {
"format": "%(asctime)s %(name)s %(levelname)s %(message)s",
"datefmt": "%Y-%m-%dT%H:%M:%S%z",
}
},
"handlers": {
"standard": {
"class": "logging.StreamHandler",
"formatter": "standard"
}
},
"loggers": {
"": {
"handlers": ["standard"],
"level": logging.INFO
}
}
}
To apply this configuration simply pass it as the parameter for the dict config:logging.config.dictConfig(config)dictConfig() will also disable all existing loggers unless disable_existing_loggers is set to False like we did in the fileConfig() example before.This configuration can be also stored in a YAML file and configured from there. Many developers often prefer using dictConfig() over fileConfig(), as it offers more ways to customize parameters and is more readable and maintainable.
import logging
import json
class JsonFormatter:
def format(self, record):
formatted_record = dict()
for key in ['created', 'levelname', 'pathname', 'msg']:
formatted_record[key] = getattr(record, key)
return json.dumps(formatted_record, indent=4)
handler = logging.StreamHandler()
handler.formatter = JsonFormatter()
logger = logging.getLogger(__name__)
logger.addHandler(handler)
logger.error("Test")
If you don’t want to create your own custom formatter, you can rely on various libraries, developed by the Python Community, that can help you convert your logs into JSON format.One of them is python-json-logger to convert log records into JSON.First, install it in your environment:pip install python-json-loggerNow update the logging configuration dictionary to customize an existing formatter or create a new formatter that will format logs in JSON like in the example below. To use the JSON formatter add pythonjsonlogger.jsonlogger.JsonFormatter as the reference for "class" property. In the formatter’s "format" property, you can define the attributes you’d like to have in the log’s JSON record:
import logging.config
config = {
"version": 1,
"disable_existing_loggers": False,
"formatters": {
"standard": {
"format": "%(asctime)s %(name)s %(levelname)s %(message)s",
"datefmt": "%Y-%m-%dT%H:%M:%S%z",
},
"json": {
"format": "%(asctime)s %(name)s %(levelname)s %(message)s",
"datefmt": "%Y-%m-%dT%H:%M:%S%z",
"class": "pythonjsonlogger.jsonlogger.JsonFormatter"
}
},
"handlers": {
"standard": {
"class": "logging.StreamHandler",
"formatter": "json"
}
},
"loggers": {
"": {
"handlers": ["standard"],
"level": LogLevel.INFO.value
}
}
}
logging.config.dictConfig(config)
logger = logging.getLogger(__name__)
Logs that get sent to the console, through the standard handler, will get written in JSON format.Once you’ve included the pythonjsonlogger.jsonlogger.JsonFormatter class in your logging configuration file, the dictConfig() function should be able to create an instance of it as long as you run the code from an environment where it can import python-json-logger module.logger = logging.LoggerAdapter(logger, {"custom_key1": "custom_value1", "custom_key2": "custom_value2"})This effectively adds custom attributes to all the records that go through that logger.Note that this impacts all log records in your application, including libraries or other frameworks that you might be using and for which you are emitting logs. It can be used to log things like a unique request ID on all log lines to track requests or to add extra contextual information.import logging.config
config = {
"version": 1,
"disable_existing_loggers": False,
"formatters": {
"standard": {
"format": "%(asctime)s %(name)s %(levelname)s %(message)s",
"datefmt": "%Y-%m-%dT%H:%M:%S%z",
},
"json": {
"format": "%(asctime)s %(name)s %(levelname)s %(message)s",
"datefmt": "%Y-%m-%dT%H:%M:%S%z",
"class": "pythonjsonlogger.jsonlogger.JsonFormatter"
}
},
"handlers": {
"standard": {
"class": "logging.StreamHandler",
"formatter": "json"
}
},
"loggers": {
"": {
"handlers": ["standard"],
"level": logging.INFO
}
}
}
logging.config.dictConfig(config)
logger = logging.getLogger(__name__)
def test():
try:
raise NameError("fake NameError")
except NameError as e:
logger.error(e)
logger.error(e, exc_info=True)
If you run test() method, it will generate the following output:{"asctime": "2020-05-10T16:43:12+0200", "name": "logging_test", "levelname": "ERROR", "message": "fake NameError"}
{"asctime": "2020-05-10T16:43:12+0200", "name": "logging_test", "levelname": "ERROR", "message": "fake NameError", "exc_info": "Traceback (most recent call last):\n File \"/Users/aleric/Projects/logging-test/src/logging_test.py\", line 39, in test\n raise NameError(\"fake NameError\")\nNameError: fake NameError"}
As we can see the first line doesn’t provide much information about the error apart from a generic message fake NameError; instead the second line, by adding the property exc_info=True, shows the full traceback, which includes information about methods involved and line numbers to follow back and see where the exception was raised.As an alternative you can achieve the same result by using logger.exception() from an exception handler like in the example below:def test():
try:
raise NameError("fake NameError")
except NameError as e:
logger.error(e)
logger.exception(e)
This can retrieve the same traceback information by using exc_info=True. This has also the benefit of setting the priority level of the log to logging.ERROR.Regardless of which method you use to capture the traceback, having the full exception information available in your logs is critical for monitoring and troubleshooting the performance of your applications.import logging.config
import traceback
config = {
"version": 1,
"disable_existing_loggers": False,
"formatters": {
"standard": {
"format": "%(asctime)s %(name)s %(levelname)s %(message)s",
"datefmt": "%Y-%m-%dT%H:%M:%S%z",
},
"json": {
"format": "%(asctime)s %(name)s %(levelname)s %(message)s",
"datefmt": "%Y-%m-%dT%H:%M:%S%z",
"class": "pythonjsonlogger.jsonlogger.JsonFormatter"
}
},
"handlers": {
"standard": {
"class": "logging.StreamHandler",
"formatter": "json"
}
},
"loggers": {
"": {
"handlers": ["standard"],
"level": logging.INFO
}
}
}
logging.config.dictConfig(config)
logger = logging.getLogger(__name__)
def test():
try:
raise OSError("fake OSError")
except NameError as e:
logger.error(e, exc_info=True)
except:
logger.error("Uncaught exception: %s", traceback.format_exc())
Running this code will throw a OSError exception that doesn’t get handled in the try-except logic, but thanks to having the traceback code, it will get logged, as we can see in the second except clause:{"asctime": "2020-05-10T17:04:05+0200", "name": "logging_test", "levelname": "ERROR", "message": "Uncaught exception: Traceback (most recent call last):\n File \"/Users/aleric/Projects/logging-test/src/logging_test4.py\", line 38, in test\n raise OSError(\"fake OSError\")\nOSError: fake OSError\n"}Logging the full traceback within each handled and unhandled exception provides critical visibility into errors as they occur in real time, so that you can investigate when and why they occurred.